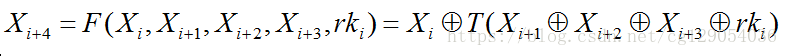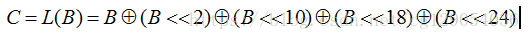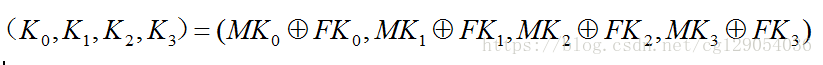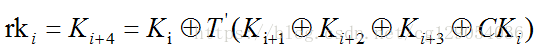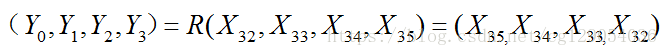各类密码学算法学习

2020-09-04

字数统计: 4.5k字 | 阅读时长≈ 17分

前几天做了几道密码学的题，感觉挺有意思的。再加之作为这个专业的学生，虽然学了密码学，但是一学就忘而且没有实践过，觉得也是一种缺陷。正好现在也需要做密码学算法，就详细完整的学习一下各类密码算法。

SM3密码杂凑算法

SM3 密码杂凑算法采用 Merkle-Damgard结构，消息分组长度为 512bit，摘要长度为 256bit。压缩函数状态为 256bit，共64步操作步骤。

SM3密码杂凑算法的初始值：

SM3密码杂凑算法的初始值共256bit，由8个32bit串联构成，具体值如下：

1
2
3

IV=7380166f  4914b2b9  1724422d7  da8a0600

   a96f30bc  163138aa   e38dee4d   b0fb0e4e

SM3杂凑算法的常量：

SM3密码杂凑算法的常量定义如下：

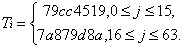
SM3密码杂凑算法的布尔函数：

SM3密码杂凑算法的布尔函数定义如下：

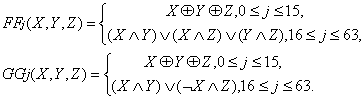
SM3密码杂凑算法的置换函数：

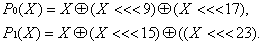
SM3密码杂凑算法的消息填充：

对于长度为 l (l < 264) 比特的消息m，SM3密码杂凑算法首先将比特 “1” 添加到消息的末尾，再添加 k 个 “0”，k是满足 l+k+1 = 448 mod 512 的最小非负整数，然后在添加一个 64 位比特串，该比特串是长度 l 的二进制表示。填充后的消息 m 的比特长度为 512 的倍数。例如：对消息 01100001 01100010 01100011，其长度 l=24，经填充得到的比特串如下：01100001 0100010 011000111 0···00···011000

SM3密码杂凑算法的迭代压缩过程：

将填充后的消息 m 按 512b 进行分组：m’=B(0)B(1)···B(n-1)，其中 n=(l+k+65)/512，对 m按如下方式迭代：

1
2
3

FOR i=0 TO (n-1)
    V(i+1)=CF(V(i),B(i));
ENDFOR

其中，CF是压缩函数，V(0) 为 256bit 初始值 IV，B(i) 为填充后的消息分组，迭代压缩的结果为 V(n)

SM3密码杂凑算法的压缩函数

SM3密码杂凑算法的压缩函数由消息扩展过程和状态更新过程组成，具体描述如下：

过程1 消息拓展过程

将消息分组 B(i) 按下一方式扩展生成 132 个字 W0, W1, … , W67, W0, W1, … , W63用于压缩函数 CF：

（1）将消息分组 B(i) 划分为 16个字 W0, W1, … W15

（2）

1
2
3

FOR j=16 TO 67
	Wj=P1(Wj-16 XOR Wj-9 XOR (Wj-3<<<15)) XOR (Wj-1<<<7) XOR Wj-6；
 ENDFOR

(3)

1
2
3

FOR j=0 TO 63
	W’j=Wj XOR Wj+4；
ENDFOR

过程2状态更新过程：

假定 A,B,C,D,E,F,G,H 为寄存器， SS1，SS2，TT1, TT2为中间变量，压缩函数 V(i+1) = CF(V(i), B(i)), 0<= i <= n-1，状态更新过程描述如下：

ABCDEFGH←V(i)；
FOR j=0 TO 63
	SS1←SS1+(A<<<12)；
	TT1←FFj(A,B,C)+D+SS2+W’j；
	TT2←GGj(A,B,C)+H+SS1+ Wj；
	D←C；
	C←B<<<9；
	B←A；
	A←TT1；
	H←G；
	G←F<<<19；
	F←E；
	E←P0(TT2)；
ENDFOR

V(i+1)←ABCDEFGH XOR V(i)

过程3杂凑值：

ABCDEFGH*←XOR *V(n)

输出 2656bit 的杂凑值 y=ABCDEFGH.

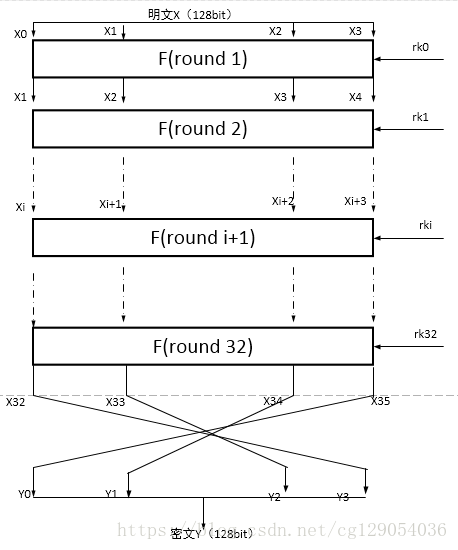
SM4加密算法

SM4算法结构图

参数产生

字节由 8 位 2 进制表示，字由 32 位 2进制数表示；
S 盒为固定的 8bit 输入盒输出置换；
加密密钥长度为 128bit，表示为 MK = (MK0, MK1, MK2, MK3)，其中 MKi (i=0,1,2,3) 为字。轮密钥表示为 rki (i=0,1,2, …, 31) 为字。 FK=(FK0, FK1, FK2, FK3) 为系统参数， CK=(CK0,CK1,CK2, …, CK31) 为固定参数，都为字。

轮密钥

整体的加密函数为：

其中 T 为一个合成置换，由非线性变换和线性变换复合而成：

非线性变换由 4个平行的S盒构成，S盒的数据采用 16进制。
线性变换公式如下，其中 B 为非线性变换得到的字

密钥拓展

已知加密密钥 MK=(MK0, MK1, MK2, MK3)，系统参数 FK=(FK0, FK1, FK2, FK3)，固定参数 CK = (CK0, CK1, CK2, …, CK31)

rki 为轮密钥，轮密钥由加密密钥生成：

首先：

然后对 i = 0,2,3, …, 31：

改变换与加密中的 T 变换基本相同，只是将其中的线性变换改为：

由于系统参数个固定参数是已知的，轮密钥既可得

加密与解密过程

加密最后一轮变换时，输出为：

最后输出是加密的反序，解密时只是将轮密钥的使用顺序进行逆向进行。

SM2加解密算法

椭圆曲线算法

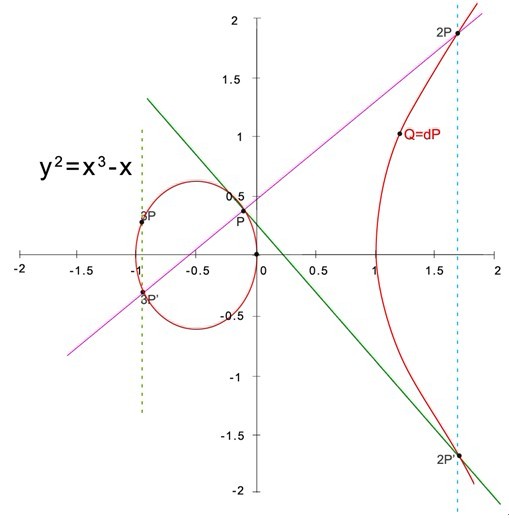
上图方程： $y^2=x^3–x$ 的曲线：

P点为基点
通过 P 点做切线，交与点 2P 点，在 2P’ 点做竖线，交与 2P 点， 2P 点即为 P点的 2倍点
同理，可以计算出 P点的 4，5，6 … 倍点
如果给定图上 Q 点是 P的一个倍点，请问 Q 是 P 的几倍点？
直观上理解，正向计算一个倍点是容易的，反向计算一个点是 P的几倍点则困难的多。
直观上理解，正向计算一个倍点是容易的，反向计算一个点是 P的几倍点则困难的多

在椭圆曲线算法中，将倍数 d 作为私钥，将 Q 作为公钥，当然椭圆曲线算法还有更严格的计算过程，相对图示要复杂的多。

SM2 算法采用的椭圆曲线方程为：

$y^2=x^3+ax+b$

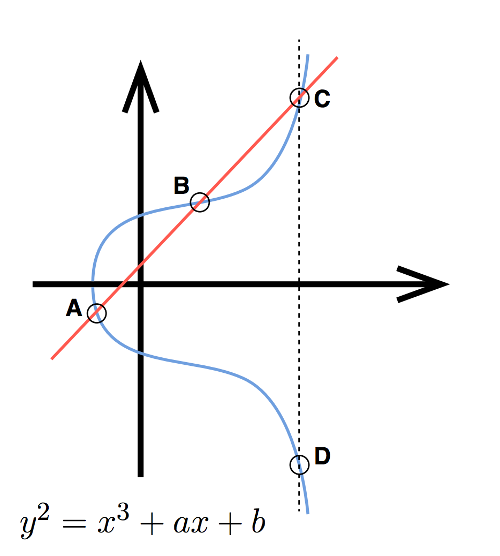
在 SM2 算法标准中，通过指定 a、b 系数，确定了唯一的标准曲线，同时为了将曲线映射到加密算法，SM2标准中还确定了其他参数，供算法程序使用

SM2系统参数

SM2 算法使用固定的 Fp 域，系统参数如下：

Fp 域的特征 p， p 是 m 比特长度的素数
Fp 中的两个元素 a 和 b，他们定义曲线 E 的方程： $y^2=x^3+ax+b$ ，a、b满足 $4a^3+27b^2≠0$
基点 $G=(x_G, y_G) ∈ E(F_p)$ ， $G≠O$ （O为无穷远点）
基点 G 的阶 n，n 是 m比特长度的素数

说明：

$p$ )、 $a$ )、 $b$ )、 $x_G$ )、 $y_G$ )和 $n$ )均为 $m$ 比特长度的大整数，也可以看作m/8字节长度的字符串。
G可以看作一个有序整数对，也可以看作一个m/4+1字节长度的字符串。
无穷远点O是一个理想点，不能用有序整数对(x, y)即仿射坐标表示。

推荐使用素数域256位椭圆曲线。
椭圆曲线方程：y ^ 2 = x ^ 3 + ax + b。
曲线参数：
p  = FFFFFFFE FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF 00000000 FFFFFFFF FFFFFFFF
a  = FFFFFFFE FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF 00000000 FFFFFFFF FFFFFFFC
b  = 28E9FA9E 9D9F5E34 4D5A9E4B CF6509A7 F39789F5 15AB8F92 DDBCBD41 4D940E93
n  = FFFFFFFE FFFFFFFF FFFFFFFF FFFFFFFF 7203DF6B 21C6052B 53BBF409 39D54123
Gx = 32C4AE2C 1F198119 5F990446 6A39C994 8FE30BBF F2660BE1 715A4589 334C74C7
Gy = BC3736A2 F4F6779C 59BDCEE3 6B692153 D0A9877C C62A4740 02DF32E5 2139F0A0

SM2密钥对生成

SM2 的密钥对包括私钥（记为d）和公钥（记为 Q），其中 d 为小于 n-1 的一个随机的正整数，Q为曲线 E(Fp) 上的一个非无穷远点且满足 Q = dG (即连续 d 个 G 点相加，简称点乘)

说明：

$E(F_p)$ )上的两个点“相加”是一个较复杂的运算过程（与普通的整数加法不同）， $O$ )与 $E(F_p)$ 上的任意点P“相加”结果仍为P，“相加”是一个可结合、可交换的运算。
$Q=(x_Q, y_Q) \in E(F_p), Q≠O$ ，可以看作一个有序整数对。

SM2加解密

SM2加密同样使用公钥，公钥由一个曲线坐标点组成，在X.509证书中的公钥表示为 04 标记开始的 2 个 32byte 的大整数，即曲线点 P(x,y) 。SM2公钥加密算法比 RSA 相对复杂，加密结果由 3 个部分组成，SM2加密过程中使用了随机数，因此同样的明文数据每一次加密结果都不一样。SM2加密算法流程如下图所示：

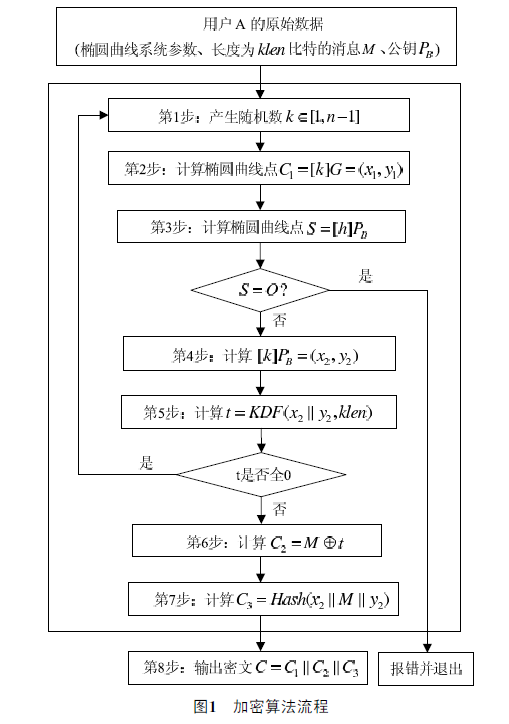
根据国密推荐的SM2椭圆曲线公钥密码算法，首先产生随机数计算出曲线点C1，2个32byte的BigInteger大数，即为SM2加密结果的第1部分。第2部分则是真正的密文，是对明文的加密结果，长度和明文一样。第3部分是杂凑值，用来效验数据。按国密推荐的256位椭圆曲线，明文加密结果比原长度会大96byte。

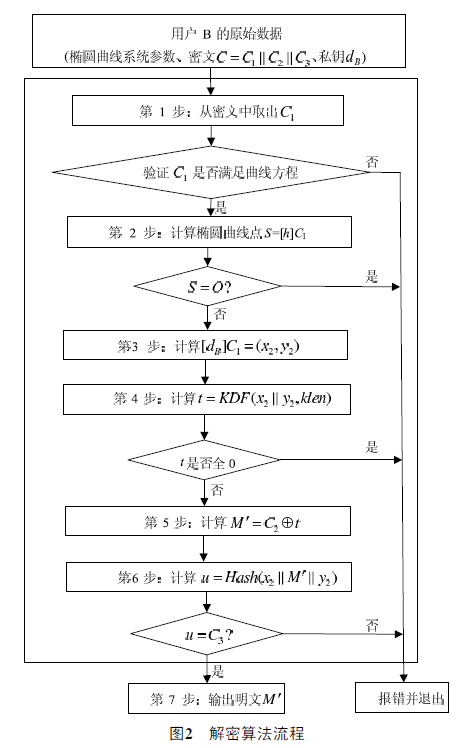
SM2解密算法

SM2解密算法是加密逆运算，首先需要从密文中取出加密结果的 3 部分值，然后通过私钥计算出 M‘ 明文值，最后校验数据。SM2解密算法流程如下：

SHA3加解密算法

输入为任意长度的字符，输出为 256 位的 hash值。可表示为：SHA3-256(M)

其中 M 为需要进行哈希计算的数据，对数据哈希的过程主要基于海绵结构(sponge construction)进行。

海绵结构

海绵结构能够进行数据转换，将任意长的输入转换为任意长的输出。如下图所示：

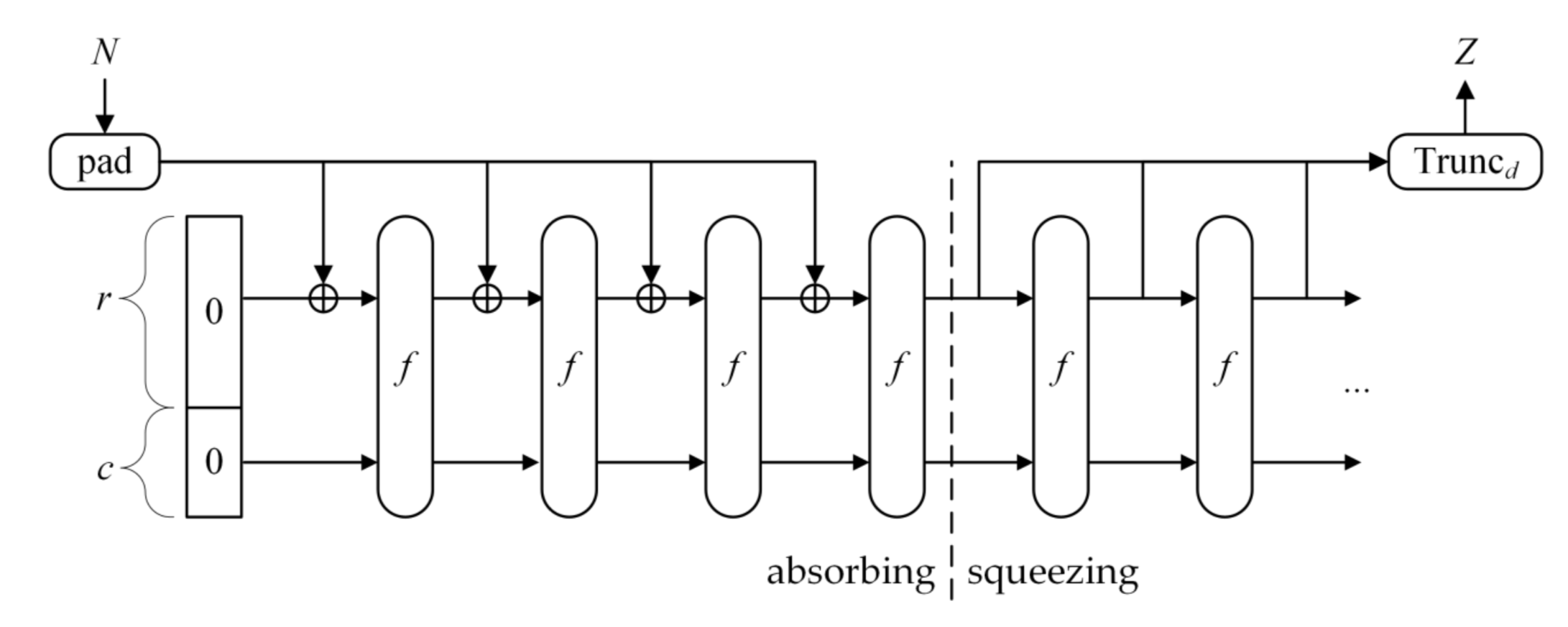
如图所示，海绵结构包含 3 个重要的组成部分：

一个对数据进行等长映射的函数 f，即输出串长度与输入串长度相同，记为b；
一个参数称为比率(rate)，记作 r，是指每轮要吸收的长度为 b 的串中数据的长度，剩余部分称为容量，记为 c，因此有 b = T+c
一个填充(padding) 函数，记作 Pad(x, m) ，返回将长度为 m 的串填充为 x 的整数倍长度的串。例如 Pad(5, 2) = 010，指将长度为 2 的串填充为 5 的整数倍长度，需要添加一个长度为 3 的串，任意长尾 3 的串均可，本例中返回值为 010，其长度为 3.

给定上述组成后，可以对数据进行操作并得到映射结果，形式化定义如下：SPONGE[f, pad, r]

下面简要说明海绵函数的执行流程：

首先对输入 N 进行填充，使其长度为 r 的整数倍，结果为 P = N||pad(r, len(N))||, “||” 表示串连接
记 n = len(P) / r，将 P 分成 n 段，记为 P = P0||P1||P2|| … || Pn-1，每段长度为 r。
定义 S = 0^b表示长度为 b 的 0 串，这个 SS 也被称为状态。
定义 i 从 0 到 n-1，对 S 依次进行转换，S=f(S⊕(P*i∣∣0c))，上述过程称为吸收 (absorbing) 过程。
定义 Z 为空串
Z=Z∣∣Trunc**r(S)，其中 Trunc_r(S)Trunc**r(S) 指 S 前 r个字符组成的串。
如果此时 d≤len(Z)，*返回** Trunc_d(Z)*。
令 S=f(S*)，返回步骤 6。

KECCAK 海绵函数

定义一个海绵结构需要指明海绵结构中的三个组成成分

一个对数据进行等长映射的函数 f。
一个参数称为比率 r。
一个填充 ( padding ) 函数，记作 pad(x,m)。

SHA-3 中使用的 KECCAK 海绵函数的三个组件形式如下：

映射函数 KECCAK-pb,n**r，将长度为 bb 的串 SS，经过 n_rn**r 轮转换输出为长度为 b* 的结果，也被称为KECCAK-p 置换函数。该函数之后会详细说明。
比率 r* 根据输出长度不同进行调整。
填充函数为pad10∗1(x,m)，除了返回将长度为 mm 的串填充为 x* 的整数倍长度的串外，还保证返回的串满足表达式10∗1 形式。

KECCAK-p 置换

KECCAK-p 置换将输入串进行多轮重新排列得到长度相同的输出串。设输入串 S 长度为 b，置换进行 nr 轮重新排列，则进行的 KECCAK-p 置换函数记为
$$
KECCAK-p b, nr
$$
其中，
$$
b\in {25, 50, 100, 200, 400, 800, 1600}b∈{25,50,100,200,400,800,1600}
$$
置换函数也可以认为是在进行状态转移，前面提到，这个函数的输入 SS 又称为状态
$$
，\mathrm {K\footnotesize ECCAK} \text{-} \normalsize{ \mathit{p}}KECCAK-p
$$
置换，就是对
$$
S
$$
进行状态转移。下面简要介绍一下状态的概念。

状态 ( state )

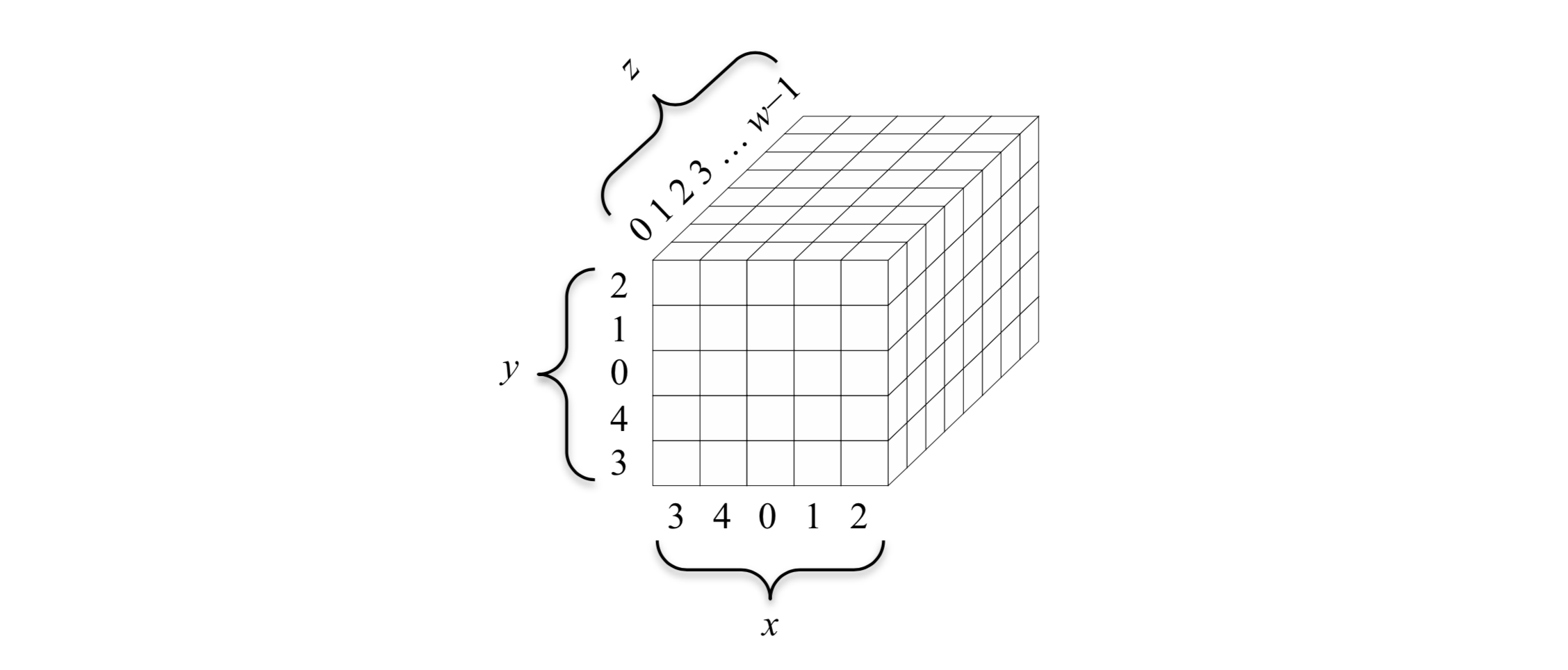
一个一直被更新的位数组称为一个*状态。一个状态可以表示成一个位串或一个状态数组。位串*就是指状态的二进制串，记为 *S，长度记为 b；状态数组将状态表示为一个
$$
5\times 5\times w
$$
的三维数组，其中 w = b/25，记为 A。*S 和 A* 都表示状态，可以互相转换。这里不详细描述有兴趣可以参看文末链接。

状态数组中的每一位可以用A[*x,y,z] 表示，状态数组的坐标系统如下所示：

其中，x，y 方向都以中心点为原点。下面是状态数组中不同子数组的命名。

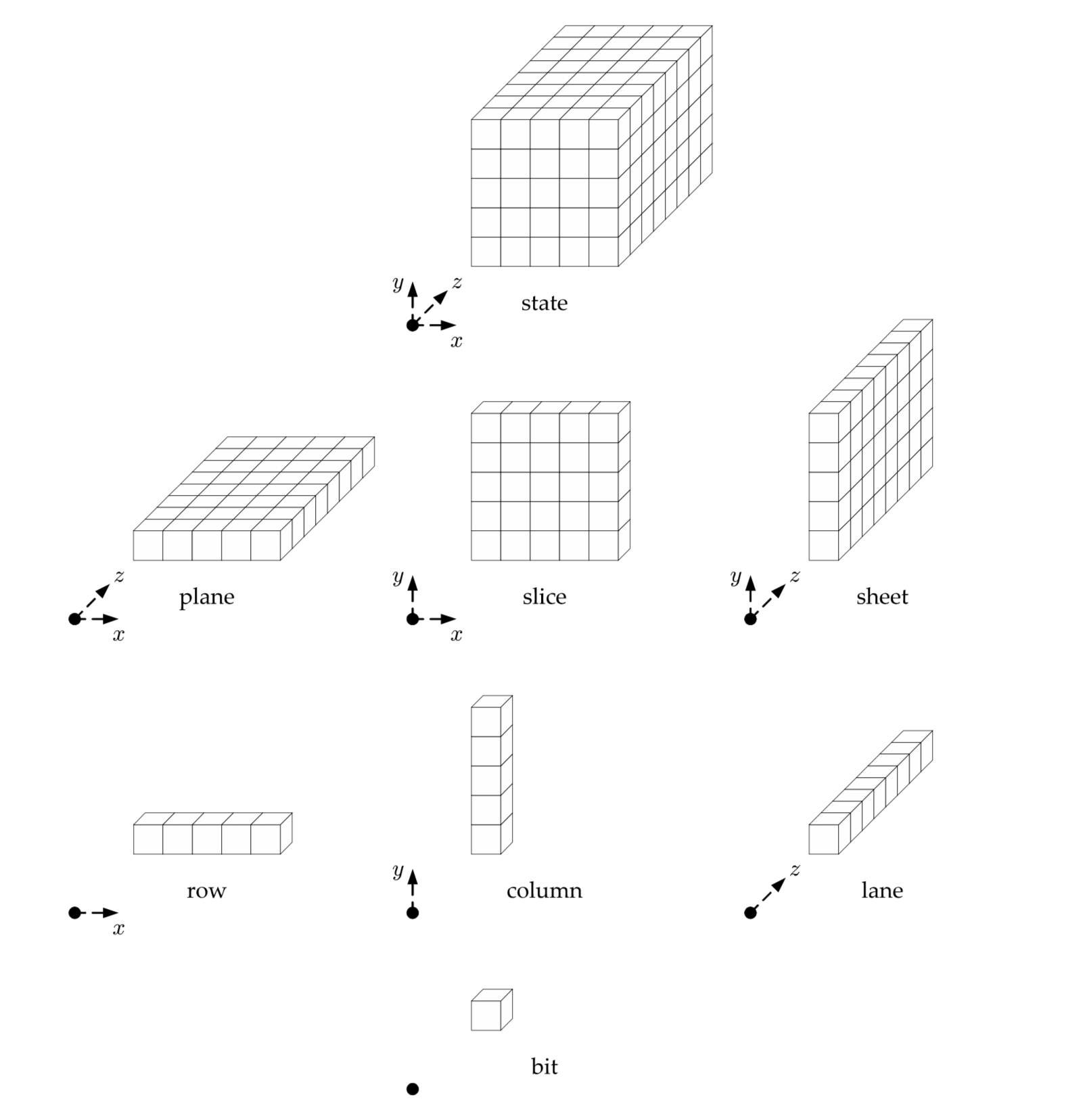
阶段映射 ( step mappings )

SHA-3 标准中共有 5 个映射函数，可以对状态数组 AA 进行不同的排列，下面简要进行介绍。

θ(A)，对 column进行重排列。
ρ(A)，对 lane进行重排列。
π(A)，对slice进行重排列。
χ(A)，对 row进行重排列。
ι(A,ir)，对 A*[0,0,z] 部分进行重排列。

对于 nr 轮转换，每一轮使用函数 Rnd 进行转换：
$$
Rnd(A,ir)= ι(χ(π(ρ(θ(A)))),ir)
$$
其中，每轮转换的
$$
i_r\in[12+2\ell-n_r,12+2\ell-1]*i
$$

置换过程

置换过程总结如下：

将 S 转换为 A
对于 ir，从 **
$$
12+2\ell-n_r
$$
取值，到12+2ℓ−1，得到 A=Rnd(A,i**r)
将 A** 转换为 S′，并返回 S′

AES加解密

AES基本结构

AES为分组密码，分组密码就是把明文分成一组组的，每组长度相等，每次加密一组数据，直到加密完整个明文。在AES标准规范中，分组长度只能是128位，即每个分组为16个字节（每个字节为8位）。密钥长度可使用128位、192位和256位。密钥长度不同，轮加密轮数也不同：

AES	密钥长度（32位比特字）	分组长度（32位比特字）	加密轮数
AES-128	4	4	10
AES-192	6	4	12
AES-256	8	4	14

以AES-128为例，密钥长度为128位，加密轮数为10轮。

AES的加密公式 C=E(K,P) ,在加密函数 E 中，会执行一个论函数，并且执行10次论函数。这个论函数的前9次执行的操作是一样的，只有第10次有所不同。也即一个明文分组会被加密10轮，AES的核心是实现一轮中的所有操作。

RC6密码算法

RC6使用的是相关数据循环移位的思想，RC5本身是一个非常快的分组密码，但其在处理128位分组块时使用 2 个 64位的工作寄存器，而AES目前在讲究效率和简洁方面不支持 64位操作，所以 RC6 对此做了修改，改用4个 32位工作寄存器，这样使得在每次循环中要做两次循环移位操作，让更多的数据位来决定循环次数。RC6中又添加了整数乘法操作，乘法操作在RC6中被用来计算循环移位的位数，使得循环移位的次数将于另一个寄存器中的所有位相关，因此 RC6 每次循环都比RC5有更快的扩散性，这使得 RC6 可以利用较少的循环次数达到要求的安全性能，从而提高了数据的吞吐能力。

ECDSA

ECDSA(Elliptic Curve Digital Signature Algorithm), 使用椭圆曲线加密算法学进行 数字签名 的一种算法.

安全等级(用bit表示其破解最大可能运算次数)，如 80bit 公钥，意味着最大可能需要 2^80 次运算才能找到私钥

在 80bit 这个安全等级上，ECDSA的公钥长度为 160bit，而DSA的公钥长度为 320bit，体量上大大缩小。

基本流程

算法的基本思路：

选择一条曲线
选择该曲线上的一个点，作为你的原点
生成一个随机数，作为你的私钥
以原点和随机数，经过一系列神奇的数学运算，得到你的公钥。

签名方法

获取需要签名的数据（或文件）的 Hash
使用私钥对该 Hash 进行签名，生成 R 和 S

验签方法

使用 S 和公钥，通过一个神奇的数学运算，生成 R‘
对比 R 和 R’，两者相同，则签名合法，否则，非法

算法原理

Hash 是数据的摘要结果，标准 ECDSA使用的 Hash 算法是 SHA1，但这个可以进行替换，如可使用 SHA3的算法进行数据摘要。这个摘要长度越大，运算量越多，安全性越高。
椭圆曲线公式 y^2 = (x^3 + a^x + b) mod p和点加法 point addition 是 ECDSA的基础
暗门函数 trapdoor function，要求单向运算简单，逆向运算困难。ECDSA属于离散对数类的暗门函数的一种。
ECDSA 算法中需要设置的参数包括：y^2 = (x^3 + a * x + b) mod p 中的 a 和 b，指定曲线 p。P 是质数，还有 N 椭圆曲线上点的个数， 0 < N < P，而且 N 是。

流程

创建签名

40字节的签名，分为 2 个部分， R 和 S，各占 20个字节

R 的生成：

生成时，需要先使用随机算法生成一个 20 字节的 k
在使用点乘法运算得到点 P， P =k*G
该P点的 X 坐标值，为 R

S 的生成：

获取数据的 Hash值，记为 z
S = k^-1 (z + dA * R) mod p，dA私钥

验证签名

P = S^-1 * z *G + S^-1 * R * Qa， Qa公钥
如果 P 的 x 坐标值等于 R，则该签名合法，否则非法

算法风险点

K 随机值，要求为加强强度随机数，如果其伪随机值可以被猜测，则有可能被破解

本文作者： A1ex
本文链接： http://yoursite.com/2020/09/04/各类密码学算法学习/
版权声明： 本博客所有文章除特别声明外，均采用 MIT 许可协议。转载请注明出处！